[size=140]Elektroniikan peruskomponenteista[/size]
Käyn tässä artikkelissa hieman läpi elektroniikan peruskomponentteja, käyttäen paikoin niinsanottua “leego-ajattelua” joidenkin asioiden havainnollistamiseen. En myöskään edes väitä oikeasti tietäväni esimerkiksi puolijohdefysiikasta juuri mitään, joten en käy asioita ihan perin pohjin läpi, vaan lähinnä luon yleiskuvan peruskomponenttien toiminnasta ja ominaisuuksista.
Käyn tässä artikkelissa läpi ainakin jollakin laajuudella seuraavat komponentit:
- resistori eli vastus
- kondensaattori
- kela
- diodi
- zener-diodi
- LED eli valodiodi
- bipolaaritransistori (BJT)
- FET-transistori
- operaatiovahvistin
[size=140]Resistori eli vastus[/size]
Vastus on yksi tavallisimmista ja yksinkertaisimmista elektroniikan komponenteista. Vastus luo virran ja jännitteen välille ohmin lain mukaisen riippuvuuden U = RI. Tästä seuraa, että vastuksen yli olevan jännitteen suhde vastuksen läpi kulkevaan virtaan on vastuksen resistanssin suuruinen, eli U/I = R. Näiden perusteella vastuksella voidaan muunmuassa 1) muuttaa virtasignaali jännitteeksi, 2) muuttaa jännitesignaali virraksi, ja 3) rajoittaa piirissä kulkevaa virtaa, joka on käytännössä sama asia kuin kohta 2).
Ohmin laki voidaan siis pyöräyttää seuraavaan kolmeen muotoon:
U = RI
I = U/R
R = U/I
Vastuksessa/kuormassa kuluva teho puolestaan saadaan kaavalla:
P = UI
Joka on virran ja resistanssin avulla: P = UI = RI * I = RI^2
Ja toisaalta jännitteen ja resistanssin avulla: P = UI = U * U/R = U^2/R
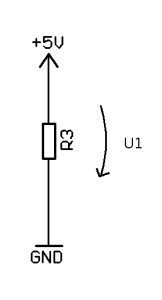
Ohmin lain ensimmäisessa muodossa voimme laskea vastuksen yli vaikuttavan jännitteen, kun tiedämme vastuksen resistanssin ja siinä kulkevan virran. Tätä voidaan käyttää esimerkiksi virranmittaukseen (“shunttivastus”), mutta tämän tavan huonona puolena on vastuksessa hukkaantuva teho, mikäli vastus ei ole hyvin pieni tai virta hyvin pieni.
Ohmin lain toisesta muodosta voimme laskea piirissä kulkevan virran jos tiedämme vastuksen yli vaikuttavan jännitteen ja sen resistanssin.
Kolmannesta muodosta voimme laskea vastuksen resistanssin, jos tiedämme sen yli vaikuttavan jännitteen ja siinä kulkevan virran. Toisinsanoen vastuksen mitoitus jännitteen ja virran perusteella (esim. LED:n etuvastus).
Edellä esitetyistä vastuksen ominaisuuksista johtuen voidaan kahdella tai useammalla vastuksella toteuttaa niinkutsuttu jännitejakokytkentä, jolla voimme tuottaa käyttöjännitteen ja nollan väliltä minkä tahansa jännitteen, muuttamalla kahden vastuksen suhdetta. Kun kytkemme kaksi vastusta R1 ja R2 sarjaan ja sitten maan ja käyttöjännitteen väliin, saamme jännitejakokytkennän.
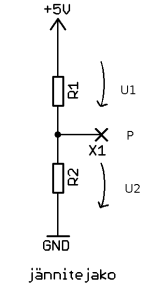
Olettaen että keskipistettä P ei kuormiteta eli siitä ei oteta virtaa mihinkään, on tällöin Kirchhoffin lain mukaan molemmissa vastuksissa kulkeva virta sama: I = U/R = U/(R1 + R2). Nyt kun tiedämme vastuksissa kulkevan virran, voimme laskea niiden yli olevat jännitteet: U1 = I*R1 ja U2 = I*R2. Tästä huomataan, että kummankin vastuksen yli oleva jännite jakautuu vastuksien resistanssien suhteessa. Voimmekin sijoittaa ensimmäisen kaavan vastuksien yli vaikuttavien jännitteiden kaavoihin, jolloin saamme:
U1 = I * R1 = U/(R1 + R2) * R1 => U1 = U * R1/(R1 + R2)
U2 = I * R2 = U/(R1 + R2) * R2 => U2 = U * R2/(R1 + R2)
Jännitejaon huono puoli on se, että sitä ei voida kuormittaa muuttamatta keskipisteen jännitettä (koska tällöin vastuksissa kulkevat virrat muuttuvat eivätkä ole enää yhtäsuuria, niin myös niiden yli olevat jännitehäviöt muuttuvat). Toisinsanoen tuotettua jännitettä voidaan käyttää vain referenssinä jollekin suuren tuloimpedanssin piirille kuten operaatiovahvistimelle.
[size=140]Kondensaattori[/size]
Kondensaattori on komponentti, joka varastoi energiaa sähkökenttään. Se koostuu kahdesta johdinlevystä tai -foliosta, joiden välissä on eristekerros. Kun näiden johdekerrosten välillä on jännite-ero, muodostuu eristeaineeseen sähkökenttä, johon varastoituu energiaa. Kondensaattorin kykyä varastoida energiaa kuvaa sen kapasitanssi, joka on kondensaattoriin varastoituneen varauksen ja kondensaattorin napojen välisen jännite-eron suhde, eli C = Q/U. kapasitanssin yksikkö on Faradi. Kondensaattoriin varastoitunut energia puolestaan on W = 0,5 * CU^2 = 0,5 * UQ. Koska kondensaattorin jännite riippuu sen varauksesta, ja varaus on kondensaattoriin kulkevan virran integraali ajan suhteen, seuraa siitä se, että kondensaattorin yli oleva jännite voi muuttua vain virran kulkiessa ja “virran jälkeen”. Tästä seuraa, että kondensaattorin voidaan ajatella läpäisevän vaihtovirtaa, koska kondensaattori varautuu ja purkautuu ja varautuu vastakkaismerkkisesti vaihtojännitteen tahdissa, kun taas tasajännitteellä kondensaattori vain aluksi varautuu käyttöjännitteeseen ja tämän jälkeen virtaa ei enää kulje.
Kondensaattorilla voidaan täten vakauttaa jännitetasoa, koska sen jännite muuttuu vasta varauksen siirryttyä eli virran kuljettua. Siksi kondensaattoreita käytetään esimerkiksi mikropiirien käyttöjännitteen suodatuksessa. Tällöin nopeat jännitepiikit, tai tarkemmin niiden aiheuttamat virrat ajautuvat suodatuskondensaattoriin ja itse käyttöjännitelinja ei ehdi heilahtaa liiaksi haittaamaan piirin toimintaa.
[size=140]Kela[/size]
Kela on komponentti, joka varastoi energiaa magneettikenttään. Kela koostuu johdinsilmukoista, joiden sisällä voi olla magneettisesti johtavasta materiaalista valmistettu sydän, tai kela voi olla myös ilmasydäminen. Kondensaattorille vastakkaisesti kela pyrkii pitämään lävitseen kulkevan virran vakiona ja sen yli oleva jännite puolestaan voi vaihdella nopeasti ja suuresti ilman, että virrassa tapahtuu vielä merkittäviä muutoksia. Se, mikä on “nopeasti”, riippuu tietysti kelan rakenteesta eli sen induktanssista, joka kuvaa sen kykyä tuottaa magneettikenttää ja varastoida energiaa magneettikenttään. Induktanssin yksikkö on Henry. Kun kelan läpi kulkeva virta muuttuu, pyrkii kela kumoamaan muutoksen tuottamalla ylitseen jännitteen, joka kumoaisi muutoksen. Kelan tuottama jännite on u(t) = L * di(t)/dt, eli mitä nopeammin virta muuttuu ja mitä suurempi on kelan induktanssi, sitä suurempi on syntyvä jännite. Tai kääntäen, eli mitä suurempi on kelan induktanssi, sitä hitaammin virta muuttuu samalla jännitteen muutoksella (tai: mitä suurempi induktanssi, sitä suurempi jännitteen muutos tarvitaan smaan virran muutosnopeuteen).
Keloja käytetään esimerkiksi suodattamaan häiriöitä (häiriövirtoja) käyttöjännitelinjasta, sekä hakkuriteholähteissä varastoimaan energiaa väliaikaisesti magneettikenttäänsä. Tällöin voidaan esimerkiksi suuresta jännitteestä tuottaa pienempi jännite lätkyttelemällä kytkintransistoria sopivalla tavalla auki ja kiinni, ja kela pitää virran vakiona ja vuorotellen ottaa energiaa tulopuolen korkeasta jännitteestä ja sitten luovuttaa sitä lähtöpuolelle. Tällöin ei tarvitse hukata energiaa lämmöksi kuten lineaarisissa teholähteissä, jotka tuottavat halutun lähtöjännitteen käytännössä muuttuvan resistanssin avulla sopivasti tehoa hukkaamalla.
[size=140]Diodi[/size]
Diodi on yhdestä PN-liitoksesta koostuva puolijohdekomponentti. Sillä on se ominaisuus, että se sallii virran kulkea vain yhteen suuntaan. Myötäsuuntaan diodi on kytketty silloin, kun sen anodi on positiivisessa jännitteessä verrattuna sen katodiin. Virta alkaa kulkea, kun diodin yli myötäsuuntaan oleva jännite ylittää diodin kynnysjännitteen. Myötäsuunnassa diodin yli jää sen rakenteesta ja materiaalien ominaisuuksista riippuen jännitehäviö nimeltään kynnysjännite, joka vaihtelee n. 0,2V ja 2V väliltä. Suuremmat jännitehäviöt ovat yleensä tehoelektroniikan suuria estosuuntaisia jännitteitä ja suuria myötäsuuntaisia virtoja kestävillä diodeilla. Normaali jännitehäviö ns. pienillä diodeilla on 0,6…0,7V. Schottky-diodeilla on pieni jännitehäviö, esimerkiksi vain 0,2V, ja ne ovat usein nopeampia (pienempi reverse recovery aika) kuin “tavalliset” diodit.
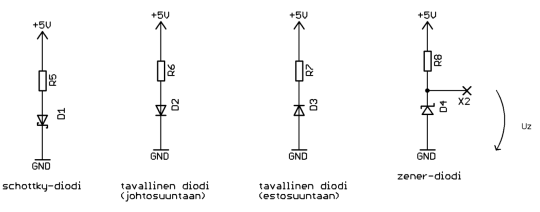
Diodeja käytetään esimerkiksi vaihtojännitteen tasasuuntaukseen, sekä hakkureissa tai muutoin kelojen yhteydessä ns. free-wheeling-diodeina, jolloin ne sallivat kelaan varastoituneen energian siirtyä virtana jonnekin eteenpäin.
[size=140]Zenerdiodi[/size]
Zener-diodi on diodin variaatio, jossa hyödynnetään sen erityisiä estosuuntaisia ominaisuuksia. Myötäsuuntaan zenerdiodi toimii aika pitkälti samoin kuin normaali diodi, mutta estosuunnassa sillä on ominaisuus, että se sallii virran kulkea kun tietty ns. zener-jännite ylitetään. Täten se siis pitää ylitsensä olevan jännitteen suhteellisen vakiona sen jälkeen kun zener-jännite on saavutettu.
Zener-diodia voidaan tämän ansiosta käyttää esim. suojaamaan piiriä ylijännitepiikeiltä (ei kuitenkaan paras ratkaisu siihen tarkoitukseen), tai luomaan referenssijännitteitä tai hyvin pienessä mittakaavassa tuottamaan reguloitu lähtöjännite. Reguloinnissa zener-diodin avulla on se ongelma, että zener-diodi on kytkettynä sarjaan virtaa rajoittavan vastuksen kanssa ja kuorma on zener-diodin rinnalla. Koska zener-diodi luo ylitseen vakiojännitteen, tarkoittaa se, että vastuksen läpi kulkee virta, joka riippuu jännitelähteen ja zener-jännitteen erosta jaettuna vastuksen koolla. Eli jos kuorma yrittää ottaa virtaa enemmän kuin tuo laskennallinen vastuksen läpi kulkeva virta on, putoaa lähtöjännite alle zener-jännitteen (jännitehäviö syntyy vastuksen yli) ja zener-diodi ei tällöin enää vaikuta millään tavalla ja regulointi on menetetty. Toisaalta jos vastuksen arvoa pienennetään jolloin saataisiin suurempi lähtövirta, jos kuorma ei otakaan virtaa, niin kulkee kaikki tuo virta tällöin itse zener-diodin läpi (koska se yrittää pitää jännitteen zener-jännitteen arvossa), joka puolestaan lämpenee teholla P = UI, jossa U on zener-jännite. Tämä siis tarkoittaa myös, että zener-reguloitu kytkentä ottaa koko ajan samaa virtaa/tehoa (mikäli ei mennä alle zener-jännitteen), riippumatta siitä meneekö virtaa ollenkaan kuormaan. Tilannetta saadaan parannettua kytkemällä mukaan bipolaaritransistori vahvistamaan virtaa, mutta ei nyt mennä siihen sen pidemmälle.
[size=140]LED eli valodiodi[/size]
LED eli valodiodi on varmasti kaikille elektroniikka-harrastajille tuttu komponentti. Välillä LED tuntuu olevan koko harrastuksen ainoa valopilkku… 
LED eli Light Emitting Diode on siis periaatteessa kuin tavallinen diodi, mutta sen valmistukseen on käytetty sellaisia materiaaleja, että elektronien kulkiessa PN-liitoksen läpi, tuottavat ne aukkoihin pudotessaan valoa. Ledejä löytyy aina pienistä SMD-merkkiledeistä suuriin useiden wattien tehoisiin teholedeihin valaistuskäyttöön. Ja variaationa kun PN-liitoksen kotelomateriaali leikataan sopivalla tavalla jotta syntyy peili ja puoliläpäisevä peili, onkin saatu laser-diodi.
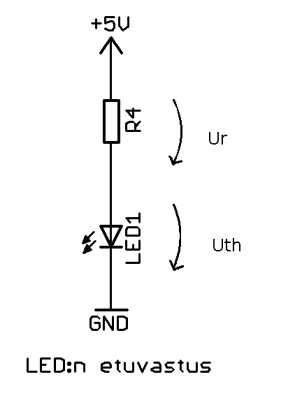
Koska LED on rakenteeltaan diodi, on sillä täten tietty kynnysjännite kuten tavallisella diodillakin. Eli virta alkaa kulkea ja valoa syntyä, kun kyseinen kynnysjännite ylitetään. Koska ledillä, kuten diodillakin, on hyvin pieni sisäinen resistanssi sen jälkeen kun kynnysjännite on ylitetty ja virta alkaa kulkea, tarvitaan virtaa rajoittamaan esimerkiksi etuvastus tai erityinen hakkurikytkentä joka tuottaa vakiovirran (LED-driver). Jos kytkemme ledin vaikka 9V:n paristoon ilman etuvastusta, rajoittaa virtaa tällöin lähinnä pariston sisäresistanssi, joka on luokkaa alle ohmin. Tästä seuraa, että virta on pienen hetken aikaa hyvin suuri, ja sitten ledi päästää toimintasavut ulos.
Normaalin 5mm:n LED:n suurin sallittu jatkuva virta voi olla esimerkiksi luokkaa 20mA. Täten on LED:n etuvastus mitoitettava käytettävän jännitteen sekä itse LED:n kynnysjännitteen perusteella. LED:n kynnysjännite vaihtelee mm. LED:n värin eli valmistusmateriaalien mukaan. Punaisen, vihreän ja keltaisen LED:n kynnysjännite voi olla luokkaa 1,6…2,2V ja sinisellä LED:llä esimerkiksi 3,8V.
Otetaanpa etuvastuksen mitoitusesimerkki:
Käyttöjännite U = 5V
punainen LED, kynnysjännite Uth = 1,8V
haluttu virta I = 10mA
U = RI => R = U/I
Koska laskemme ohmin lain avulla vastuksen arvoa tietylle virralle, olemme siis kiinnostuneita nimenomaan vastuksen yli olevasta jännitteestä Ur
Ur = (U - Uth) = 5 - 1,8V = 3,2V
R = Ur/I = 3,2V / 0,01A = 320 ohm
Jos ei laskettua vastusarvoa löydy suoraan, kannattaa yleensä mennä varman päälle ja ottaa seuraavaksi suurempi vastuksen arvo, jolloin virta jää laskettua pienemmäksi.
[size=140]Bipolaaritransistori (BJT)[/size]
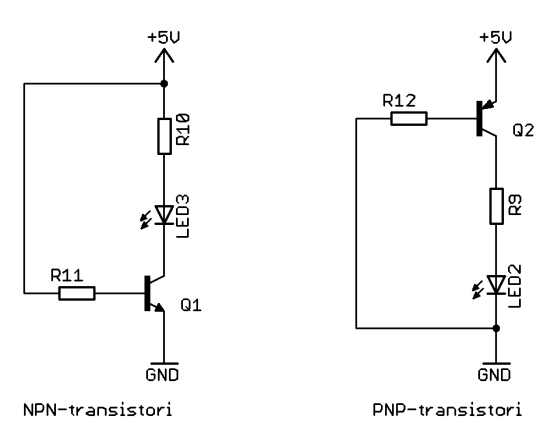
BJT-transistori eli Bipolar Junction Transistor on kahdesta PN-liitoksesta koostuva kolminapainen komponentti, jolla on se ominaisuus, että se vahvistaa sen kannalle tuotua virtaa. Eli kun kannan (base) ja emitterin välillä kulkee (pieni) virta, voi tällöin kollektorin ja emitterin välillä kulkea paljon suurempi virta. Virtojen suhdetta kuvaa transistorin virtavahvistuskerroin, joka on abauttiarallaa datalehdistä löytyvä hfe-parametri. BJT-transistorit jakautuvat kahteen päätyyppiin: NPN ja PNP, jotka kuvaavat sen rakennetta eli puolijohteen tyyppiä N tai P. Käytännössä tämä tarkoittaa, että transistoria on käytettävä eli se on biasoitava sen mukaan kumpi tyyppi on käytössä. NPN-tyypillä kulkee ohjausvirta kannalle sisään ja emitteriltä ulos, ja päävirta kollektorille sisään ja emitteriltä ulos (eli käytettäessä perinteistä virran suunnan määritelmää eli virta kulkee positiivisesta negatiiviseen päin). PNP:llä puolestaan ohjausvirta kulkee emitterille sisään ja kannalta ulos ja päävirta emitteriltä sisään ja kollektorilta ulos. Muistisääntönä vaikka niin, että NPN-tyyppinen kytketään yleensä negatiiviselle puolelle ja sitä ohjataan positivisella jännitteellä ja PNP-tyyppinen kytketään positiiviselle puolelle ja sitä ohjataan negatiivisella jännitteellä, eli “N kiinni N:ään ja P kiinni P:hen”. (tulipa huonosti selitettyä)
[size=140]FET-transistori[/size]
FET-transistori (Field Effect Trasistor) on toinen transistorityyppi, jota ohjataan hilan jännitteellä. Erilaisia FET-transistorityyppejä on lukuisia, esimerkiksi JFET ja MOSFET. FET-transistori on myös kolminapainen komponentti ja sitä ohjataan source ja gate (lähde ja hila) -napojen välisellä jännitteellä. Kun kyseinen jännite saavuttaa jonkin arvon, alkaa virta kulkea nielun ja lähteen (drain ja source) välillä. FET-transistoreita on tämän suhteen kahta tyyppiä: avaus- ja sulkutyyppiä, eli transistori voidaan joko käskeä johtamaan virtaa tai se voidaan käskeä katkaisemaan virta. Toisin kuin BJT:llä, FET-transistorin ohjaaminen ei siis vaadi virtaa muuta kuin muutostilanteessa transistorin sisäisen rakenteen pienen kapasitanssin lataamiseen tai purkamiseen. Toisaalta jos kytkentätaajuus on suuri, niin siitäkin syntyy kyllä nopeasti suurikin virta kun kyseistä kapasitanssia vuorotellen ladataan ja puretaan.
Koska FET-transistorin hila on erotettu puolijohdetasolla hyvin ohuella eristekerroksella virtaa kuljettavasta osasta, ovat FET-transistorit erittäin herkkiä staattiselle sähkölle. Suurin sallittu hilajännite on yleensä vain muutamia voltteja ja maksimissaankin luokkaa 20-30V (joka on jo FET:lle paljon), ja jos se saa vaikka “kissasähköstä” pienenkin tällin jolloin syntyy läpilyönti eristekerroksessa, on kyseinen komponentti tämän jälkeen entinen. Ja koska suurin osa nykyisistä mikropiireistä ja mikrokontrollereista ja -prosessoreista jne valmistetaan nykyään CMOS-tekniikalla (eli ne sisältävät suuret määrät FET-transistoreita), ovat ne kaikki alttiita staattisesta sähköstä hajoamiselle.
(Heitänpä tähän väliin esimerkin yliopistolta eräältä kurssilta yhden luennon lopulta: hieraisemalla kerran tavallisen college- taimikälie paidan hihaa mahaa vasten, näytti sähkökentän voimakkuutta mittaava mittari n. kilovoltin luokkaa hihalle. Korvataan tuohon yhtälöön villapaita tai kissa niin ollaan hyvin äkkiä kymmenissä kilovolteissa. Toisinsanoen ei kannata hieroa niitä FET-transistoreja tai aaveeärriä hihaan!!)
[size=140]Operaatiovahvistin[/size]
Operaatiovahvistin on analogiaelektroniikassa varsin yleinen ja hyödyllinen komponentti. Se on hyvin suuren vahvistuksen omaava differentiaali- eli erotuloinen jännitevahvistin. Se tuottaa lähtöönsä jännitteen, joka on ilman takaisinkytkentää teoriassa ääretön, ja käytännössä luokkaa satoja tuhansia kertoja suurempi kuin jännite-ero sen tuloissa. Useimpiin tarkoituksiin saadaan siitä hyödyllinen komponentti vasta, kun käytetään negatiivista takaisinkytkentää eli kytketään sen lähtö jollakin tapaa takaisin sen tuloon siten, että lähdön muuttuminen pyrkii kumoamaan tulosignaalia, eli tarkemmin sanottuna pyrkii ajamaan sen tulot samaan potentiaaliin, jolloin sen lähtö stabiloituu senhetkiseen arvoonsa.
Kun operaatiovahvistimen positiivinen eli ei-invertoiva tulo on suuremmassa jännitteessä kuin sen negatiivinen eli invertoiva tulo, on sen lähtö tällöin teoriassa positiivinen ääretön. Jos taas sen negatiivinen eli invertoiva tulo on suuremmassa positiivisessa jännitteessä kuin sen positiivinen eli ei-invertoiva tulo, on lähtö teoriassa negatiivinen ääretön. Käytännössä lähtö on edellä mainituissa tilanteissa lähellä komponentille tuotuja käyttöjännitteen ääriarvoja. “Tavallisella” oparilla lähtöjännite jää n. 0.7V tai enemmänkin käyttöjännitteen ääriarvoista johtuen reaalisten komponenttien rajoitteista. Niinkutsutuilla rail-to-rail opareilla päästään hieman lähemmäs käyttöjännitettä.
Kun operaatiovahvistimen lähtösignaali yhdistetään niinsanotun takaisinkytkennän avulla sen tulopuolelle, saadaan lähtösignaalin muutoksella muutettua sen tulosignaaleja. Muutos pyritään tekemään siten, että molemmat tulot ajautuvat samaan potentiaaliin, jolloin oparin lähtö stabiloituu kyseiseen arvoon. Näin voidaan tuottaa mm. haluttu vahvistus tulosignaalille. Kun takaisinkytkentää suunnitellaan, voidaan yleensä olettaa, että oparin tuloihin ei kulje virtaa, koska niiden tuloimpedanssi on hyvin suuri. Täten takaisinkytkentä tehdään yleensä jonkinlaisen jännitejaon ja vastusten avulla, ja mikäli tarvitaan ajan suhteen muuttuvia ilmiöitä, voi mukana olla esim kondensaattoreita (esim. aktiivinen ali- tai ylipäästösuodin, integraattori, derivaattori, …).
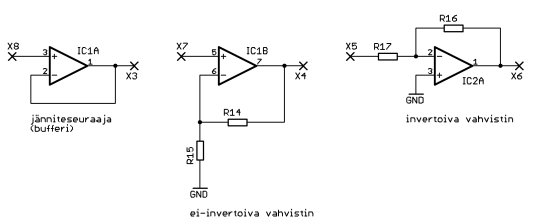
Esimerkkikuvassa invertoivan vahvistinkytkennän lähtöjännite Vout = Vin * (R16/R17), ei-invertoivan kytkennän lähtöjännite on Vout = Vin * (1 + R14/R15) ja jänniteseuraajan tapauksessa lähtöjännite on sama kuin tulojännite. Jänniteseuraaja on hyödyllinen, mikäli tulosignaalia ei voida kuormittaa paljoa ilman että sen arvo muuttuu. Koska operaatiovahvistimen tuloimpedanssi on hyvin suuri ja lähtöimpedanssi pieni, voidaan jänniteseuraajakytkentää käyttää puskuroimaan heikkoja tulosignaaleja.
[size=130]Muutoshistoria[/size]
2011-03-30 01:07: Ensimmäinen versio
2011-03-30 12:00: Lisäyksiä ja selvennyksiä operaatiovahvistimen kuvaukseen
Toivottavasti en sössinyt mitään suurempia… Kommentteja, korjauksia ja parannusehdotuksia vastaanotetaan.